basics of automata theory

 Introduction to Automata Theory's Foundations

The fascinating theoretical area of computer science known as automata theory. It got its start in the 20th century, when mathematicians started creating machines that mimicked certain aspects of humans and could perform computations more rapidly and accurately. The word "automaton" itself, which is closely related to the term, refers to automatic processes that carry out the creation of particular processes. Automata theory, as its name suggests, is concerned with the logic of computation with respect to simple machines, or automata. Computer scientists can better understand how machines compute functions and solve problems by using automata, as well as what it means to define a function as computable or to describe a question as decidable.

Robots are conceptual models.

Automatons are simplified representations of machines that operate on inputs by switching between several states or configurations. A transition function chooses the following configuration based on a finite portion of the current configuration at each stage of the computation. As a result, the algorithm accepts that input when it reaches an accepted configuration. The Turing machine is the most all-encompassing and potent automaton.

The development of techniques for computer scientists to define and evaluate the dynamic behaviour of discrete systems with periodically sampled signals is the main goal of automata theory. The arrangement of the system's storage and combinational components affects how these distinct systems behave. These machines' characteristics include:

Assumed to be a finite set I of input signals in the form of symbol sequences. The set I is specifically the set x1, x,2, x3,... xk, where k is the total number of inputs.

Sequences of symbols drawn from a finite set Z are the outputs. Set Z is the collection of values y1, y2, y3,..., ym, where m is the total number of outputs.

States: A finite set Q, the definition of which varies according on the type of automata.

The four main families of automatons are as follows:

Finite-state apparatus

Pushdown machines

Automata with linear bounds

Turing device

The families of automata mentioned above can be seen as a hierarchal structure, with the finite-state automata being the most basic and the Turing machine being the most sophisticated. The finite-state machine is the main topic of this project.

Finite automata's fascinating history as a subfield of computer science demonstrates the breadth of its potential uses. A group of biologists, psychologists, mathematicians, engineers, and early computer scientists were among the first to examine the idea of a finite-state machine. They all had the same goal in mind: to simulate human mental processes in either the brain or computers. Two neurophysiologists named Walter Pitts and Warren McCulloch were the first to describe finite automata in 1943. Their article, "A Logical Calculus Immanent in Nervous Activity," produced important advances in the fields of cybernetics, automata theory, neural network theory, and computation theory. Later, the idea was generalised by two computer scientists, G.H. Mealy and E.F. Moore.

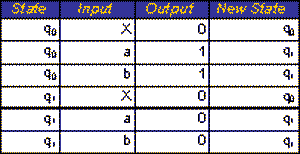
A finite-state machine is an automaton whose state set Q only has a limited number of elements (FSM). FSMs are abstract machines made up of a state transition function, a number of states (set Q), a number of input events (set I), a number of output events (set Z), and a number of input events. The state transition function returns the new set of output events and the following state after receiving the current state and an input event. As a result, it can be thought of as a function that converts an ordered series of input events into a corresponding series, or set, of output events.

I Z is the state transition function.

Finite-state machines do not preserve memory and are the best computation models for limited amounts of memory. the mathematical formulation

Think of an elevator example to fully comprehend the concept of a finite-state machine:

An elevator is a device that only keeps track of the current floor, the direction of movement (up or down), and the collection of unfulfilled service requests. It does not keep track of all prior service requests. As a result, an elevator's operation at any given time might be described mathematically by the following terms:

States: A limited number of states that reflect the history of the requests made by clients.

Inputs: Depending on how many levels the elevator can reach, the inputs are a finite set. The set I, whose size equals the number of storeys in the building, can be used.

output: Finite set of outputs that are dependent on whether or not the elevator needs to move up or down in order to meet customer needs.

Formally, a finite-state machine is a 5-tuple (Q, I, Z,, W) such that:

Q is a limited number of states.

I = a small number of input symbols

Z = a limited collection of output symbols

I x Q Q, where is the state transition function, maps I x Q into Q.

W, often known as the output function, is the mapping of I x Q onto Z.

Where F is a subset of Q, then A is the set of accept states.

A finite-state machine has a finite number of states, according to the previous mathematical understanding. Each state has rules that specify how the machine will behave for each input, and these rules are expressed in the state transition mapping function. Each state accepts a limited number of inputs. The machine might change states simultaneously in response to an input. There is exactly one transition out of each state for each input symbol. Furthermore, deterministic finite automata accept any 5-tuple set that is accepted by nondeterministic finite automata.

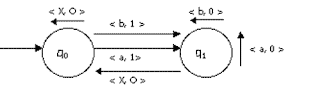
The internal states of an FSM contain no additional structure because they have finite, constant quantities of memory. State diagrams are a simple way to represent them, as shown below:

The state diagram shows how an automaton functions. Nodes in graphs are used to indicate states, arrows or branches are used to describe transitions, and symbols are used to represent the corresponding inputs and outputs. The arrow coming from the left into q0 demonstrates that q0 is the machine's initial state. Arrows on the sides of individual nodes represent moves that don't involve state changes. Self-loops are the name given to these arrows.

There are various different kinds of finite-state machines, which can be grouped into three groups:

transducers: produce output from supplied input

 acceptors: either accept the input or do not

 recognizers: either recognise the input or do not

It's crucial to remember that the internal mechanical mechanism of automata that results in the calculation of outputs and state changes is not mechanical while thinking about finite-state machines.

There are many fields where finite-state machines are used. They can function on languages with finite word counts (standard case), infinite word counts (Rabin automata, Brche automata), different kinds of trees, and hardware circuits where the input, state, and output are bit vectors of a defined size.

Turing machines vs. finite states

A finite automaton is the most basic automaton used for computation. It is not a sufficient computation model because it can only compute very simple functions. A finite-state machine's capacity is further limited by its inability to generalise calculations.

An illustration of the distinction between a finite-state machine and a Turing machine is as follows:

Think of a modern CPU. A machine's bits can only exist in two states (0 or 1). There are only a finite number of potential states as a result. Additionally, there are a limited amount of inputs from the computer's mouse, keyboard, hard drive, various slot cards, etc. when thinking about the components a CPU interacts with. It follows that a CPU can be represented as a finite-state machine.

Consider a computer right now. There are an endless amount of interactions within the computer as a whole, despite the fact that each bit in a machine can only be in one of two states (0 or 1). Within the limitations of a finite-state model, modelling a computer's operation becomes extremely challenging.

In order to answer the Entscheindungsproblem, eminent computer scientist Alan Turing created the first "infinite" (or unbounded) model of computation, the Turing machine, in 1936. A finite automaton or control unit with limitless storage is how the Turing machine can be conceptualised (memory). An endless number of one-dimensional arrays of cells make up its "memory." Turing's machine was created to give a clear mathematical definition of an algorithm or mechanical operation. It is essentially an abstract model of current computer execution and storage.

While an automaton is said to as finite if its model has a finite number of states and functions with a finite number of strings of input and output, infinite automata contain a "accessory" - either a stack or a tape that can be used to store additional data.

Formally, a Turing machine is defined by the set [Q,,,, q0, B, F]

One state, q0, is the beginning state of the finite collection of states Q.

The set of input symbols is = a subset of, excluding B.

a limited number of tape symbols are permitted.

= the next move function, which maps from Q x to Q x x L,R, where L and R stand for left and right, respectively, movement directions.

q0 = in set the start state to Q

B is a sign for, acting as the empty

the collection of final states F Q

As a result, the ability of the Turing machine to change symbols makes it significantly different from two-way finite automata (FSM).